Serie de Fibonacci

SUCESIÓN DE FIBONACCI

¿Sucesión? ¿Y eso qué es?

Una sucesión matemática es un conjunto ordenado de números (generalmente son números) en donde cada número se llama término.

¿Y cuál es la de Fibonacci? 

Fibonacci fue un matemático italiano del s.XII que pasó a la historia gracias a la sucesión que descubrió.  La sucesión es muy simple, una serie de números donde cada término es igual a la suma de los dos anteriores, siendo los dos primeros 0 y 1

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89…….

Como se puede comprobar, la sucesión comienza con dos “unos” y luego los términos se calculan sumando los dos valores anteriores.  Es una serie infinita como es fácil de observar.

Pues muy bien, ¿y eso sirve para algo?

Pues puede resultar sorprendente, pero esta serie aparece en la naturaleza en multitud de ejemplos.  Voy a citar cuatro ejemplos:

Ejemplo 1: reproducción de conejos

Realmente así descubrió Fibonacci esta serie.  Recibió un encargo para resolver un problema de cría de conejos, sorprendente ¿eh?.

Para comprender el origen de la serie hay que conocer dos aspectos relacionados con la cría de conejos:

·         La madurez sexual de los conejos la alcanzan al cumplir 1 mes de vida.

·         Durante su madurez sexual los conejos se aparean constantemente y la hembra siempre queda preñada.

·         Cuando la hembra da a luz siempre tiene una pareja (macho y hembra).

·         Durante la madurez sexual la hembra pare una pareja cada mes.

Los cuadrados amarillos son los conejos recién nacidos y que por tanto no podrán quedarse preñados hasta el mes siguiente. 

Los cuadrados blancos son conejos adultos y que por tanto paren una pareja cada mes.

Si contamos el número de parejas de cada mes obtenemos: 1, 1, 2, 3, 5, 8, 13, 21, 34… ¿te suena? ¡¡Efectivamente!!! ¡¡La sucesión de Fibonacci!!!

Ejemplo 2: árbol genealógico de las abejas

Sí, también se relaciona con esta serie.  Debemos tener en cuenta que en el mundo de las abejas no hace falta macho para fecundar.  Una abeja pone huevos y si han sido fecundados será una hembra, si no lo han sido será un macho.

Por tanto, un macho sólo tiene una madre, y una hembra tendrá madre y padre.  Por tanto, si partimos de una abeja hembra….

En blanco tenemos las hembras que cada una tendrá padre y madre.  En amarillo los machos que sólo tendrán madre.

Si contamos los “familiares directos” de cada abeja sale: 1, 1, 2, 3, 5, 8, 13, 21, 34… ¿te suena? ¡Eso es! ¡De nuevo aparece Fibonacci!

Ejemplo 3: Girasol

¿Y qué tiene que ver Fibonacci con los girasoles? Buena pregunta.  Para ampliar conocimientos del girasol hay que conocer que las pipas se encuentran en el centro de la flor y tienen una disposición con forma de espiral

Imágenes obtenidas de http://www.pinturayartistas.com/espirales-aureas-en-las-flores-y-plantas/

En el segundo dibujo están sobreimpresos los recorridos de las espirales.  ¡Pues bien, el número de espirales existentes en cualquier girasol del mundo siempre es un término de la sucesión de Fibonacci! Y el número de espirales en un sentido y en el contrario son dos números seguidos de la sucesión de Fibonacci, por ejemplo 55 hacia un lado y 89 hacia el otro

Ejemplo 4: Espiral de Fibonacci

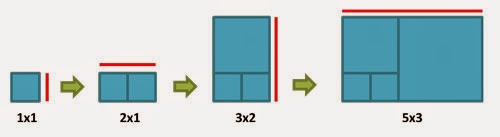
Si dibujamos un cuadrado de lado 1 y a partir de ahí le adjuntamos un cuadrado cuyo lado mida el lado mayor del rectángulo anterior obtenemos lo siguiente:

(NOTA: la línea roja marca el lado más largo del rectángulo resultante, que es donde pondremos el siguiente cuadrado)

 

Vemos que las dimensiones de los rectángulos son dos términos de la sucesión de Fibonacci.

Si ahora en cada cuadrado trazamos un arco de circunferencia interior tangente a dos lados obtenemos la espiral:

Y curiosamente esta espiral se repite en la naturaleza en múltiples ocasiones, como ejemplo nombraremos:

Disposición de pipas en el girasol

Imagen obtenida en: http://tematikas.wordpress.com/2008/10/04/matematicas-y-realidad-2/fibonacci2/

Formación de huracanes

Imagen obtenida en: http://www.taringa.net/ser22008/mi/Zoeq8

Galaxias (algunos tipos)

Imagen obtenida en: http://lightingthevoid.com/

Forma de la oreja

Imagen obtenida en: http://html.rincondelvago.com/peso-visual-y-puntos-fuertes.html

Concha del Nautilus (si no coincide con la espiral de fibonacci seguirá otra espiral logarítmica)

Imagen obtenida en: http://www.inspirationgreen.com/fibonacci-sequence-in-nature.html

Forma de un huevo

Imagen obtenida en: www.holistichouseplans.com